情報理論
■自己情報量
事象Aの起こる確率がP(A)である時、事象Aが起こることの自己情報量は、I(A)=-log2P(A)によって定義される
確率変数Xにおいて、X=xとなる確率がP(x)で与えられている時、確率変数Xのエントロピーは以下で与えられる。
エントロピーは情報量の期待値であり、確率変数のランダム性の指標としてよく用いられる。
■カルバックライブラーダイバージェンス
2つの確率分布の近さを表現する最も基本的な量である。
2つの確率分布p(x)とq(x)に対して、以下の式で表される。
■クロスエントロピー
二つの確率分布P(x)とQ(x)に対するクロスエントロピーは以下のように定義される。
このクロスエントロピーは分類問題を解くときの損失関数として使用される。
ソフトマックス関数と組み合わせると逆伝播が簡単に表せることがメリット。
確率・統計
■条件付き確率
ある事象Xが起きるという条件の元で、事象Yが起こる確率。 P(Y|X)=P(X∩Y)/P(X) 最初はなぜP(X)が分母に来るのか分からなかったが、ベン図を書いてみると理解ができた。 ベイズの定理に繋がる大事な公式。条件付き確率を変形し、導くことが出来る。
■ベイズの定理
P(YlX)=P(Y)P(XlY)/P(X) ただの式変形ではなく、事後確率P(Y|X)が事前確率P(Y)と尤度関数P(XlY)の積で表せることにある。 尤度関数は新しいデータによって更新することができるので、予測を扱う機械学習と相性が良い。
■確率変数
ある現象がいろいろな値を取るとき、とりうる値全てを確率変数Xで表す。
サイコロを例にすると確率変数は、
X ={1,2,3,4,5,6}
と表される。
■確率分布
ある事象が発生する確率を分布で表したもの。
有名な確率分布として、二項分布や正規分布、ポアソン分布などがある。
■期待値
確率変数とその確率を乗算し、確率分布全てにおいて和をとったもの。
その確率分布において、もっともらしい値を示す。
■分散・偏差
サンプリングしたデータとその平均値の差をとり、平均したもの。
データのばらつき具合を表す。
分散はデータを二乗しており、元の次元と合わないため、平方根をとった偏差sを使用することがある。
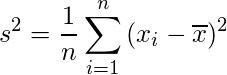
■ベルヌーイ分布
何かを行った時に起こる結果が二つしかない試行のこと。 コイントスがわかりやすい(表と裏しか起きない) P(X|μ)=μ^X×(1-μ)^(1-μ) ロジスティック回帰などの二値分類でよく見かける。 マルチヌーイ分布は拡張版で、他クラス分類等で使用する。
■正規分布
中心極限定理より、どんな確率分布でもその平均値に対しては正規分布を取ることからもっともよく見かける確率分布。
線形代数学
この記事はStudy-AI社、ラビットチャレンジのレポートを目的として執筆しています。
■ベクトルとスカラー
・スカラー:値の大小のみを示すもの
例)温度、質量、面積、長さetc...
・ベクトル:値の大きさ、向きなど2つの情報を持つもの
例)力、運動量、速度etc...
※テンソルは2つ以上の情報を持つ概念であり、ベクトルはテンソルの概念の一部である。
テンソルの例)応力、剪断力etc...
■行列
・スカラーを表にしたもの、ベクトルを並べたものである
■逆行列
ある行列Aに対して、逆行列A^-1を右から乗算すると、
AA^-1 = I(Iは単位行列)
となるもの。
余因子展開や掃き出し法を使って、逆行列を求めることができる。
ある正方行列Aに対して、あるベクトルxをスカラー倍するようなものを考える。
Ax =λx(λはスカラー)
これを用いることにより、A^nの計算が簡単になったり、固有直交分解が可能になる。
固有値分解を拡張したもの。
m×nの行列Bに対して、転置行列B^Tを用いて、A =BB^Tという正方行列を作り、行列Aに対して固有値分解をする。
